|
|
|
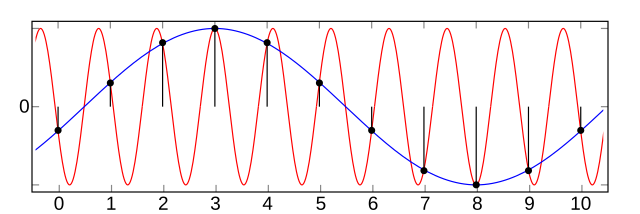
@@ -46,12 +46,12 @@ Consider the high-frequency sine wave in red. |
|
|
|
If the signal is sampled every integer, its unique reconstruction is the signal in blue, which has completely different harmonic content as the original signal. |
|
|
|
If correctly bandlimited, the original signal would be zero (silence), and thus the reconstruction would be zero. |
|
|
|
|
|
|
|
[](https://en.wikipedia.org/wiki/File:AliasingSines.svg) |
|
|
|
[](https://en.wikipedia.org/wiki/File:AliasingSines.svg) |
|
|
|
|
|
|
|
A square wave has harmonic amplitudes $\frac{1}{k}$ for odd harmonics $k$. |
|
|
|
However, after bandlimiting, all harmonics above $f_{sr}/2$ become zero, so its reconstruction should look like this. |
|
|
|
|
|
|
|
[](https://en.wikipedia.org/wiki/File:AliasingSines.svg) |
|
|
|
[](https://en.wikipedia.org/wiki/File:Gibbs_phenomenon_50.svg) |
|
|
|
|
|
|
|
The curve produced by a bandlimited discontinuity is known as the [Gibbs phenomenon](https://en.wikipedia.org/wiki/Gibbs_phenomenon). |
|
|
|
A DSP algorithm attempting to model a jump found in sawtooth or square waves must include this effect, such as by inserting a minBLEP or polyBLEP signal for each discontinuity. |
|
|
|
@@ -78,7 +78,7 @@ The filter is "linear" because the filtered sum of two signals is equal to the s |
|
|
|
|
|
|
|
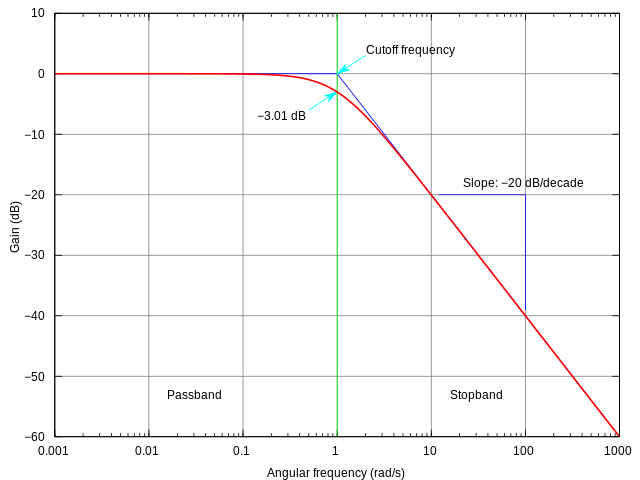
A log-log plot of $H(i \omega)$ is called a [Bode plot](https://en.wikipedia.org/wiki/Bode_plot). |
|
|
|
|
|
|
|
[](https://en.wikipedia.org/wiki/File:Butterworth_response.svg) |
|
|
|
[](https://en.wikipedia.org/wiki/File:Butterworth_response.svg) |
|
|
|
|
|
|
|
To be able to exploit various mathematical tools, the transfer function is often written as a rational function in terms of $s^{-1}$ |
|
|
|
$$H(s) = \frac{\sum_{p=0}^P b_p s^{-p}}{\sum_{q=0}^Q a_q s^{-q}}$$ |
|
|
|
|