Add initial DSP writeup

DSP.md

@@ -1,14 +1,132 @@
 # DSP
 
-Digital Signal Processing is the field of mathematics and programming regarding the discretization of continuous signals in time and space.
+Digital signal processing (DSP) is the field of mathematics and programming regarding the discretization of continuous signals in time and space.
 One of its many applications is to generate and process audio from virtual/digital modular synthesizers.
 
 There are many online resources and books for learning DSP.
 
-- https://en.wikipedia.org/wiki/Digital_signal_processing
-- https://www.dsprelated.com/
-- https://dsp.stackexchange.com/
-- https://ocw.mit.edu/resources/res-6-008-digital-signal-processing-spring-2011/
-- http://dspguide.com/
+- [Digital signal processing](https://en.wikipedia.org/wiki/Digital_signal_processing)
+- [DSPRelated.com](https://www.dsprelated.com/)
+- [Signal Processing Stack Exchange](https://dsp.stackexchange.com/)
+- [Digital Signal Processing MIT OpenCourseWare](https://ocw.mit.edu/resources/res-6-008-digital-signal-processing-spring-2011/)
+- [The Scientist and Engineer's Guide to Digital Signal Processing](http://dspguide.com/) by Steven W. Smith
+- [The Art of VA Filter Design](http://www.native-instruments.com/fileadmin/ni_media/downloads/pdf/VAFilterDesign_2.0.0a.pdf) by Vadim Zavalishin (PDF)
 
-More modular synthesizer-specific content will be added here in the future.
+Below are my mindless ramblings of various topics with a focus on DSP for modular synthesizers.
+Eventually this will become organized, but it is currently a *work-in-progress*.
+If anything here is inaccurate, you can [edit it yourself](https://github.com/VCVRack/manual) or [open an issue](https://github.com/VCVRack/manual/issues) in the manual's source repository.
+Image credits are from Wikipedia.
+
+
+### Sampling
+
+A *signal* is a function $f(t): \mathbb{R} \rightarrow \mathbb{R}$ of amplitudes (voltages, sound pressure levels, etc.) defined on a time continuum, and a *sequence* is a function $f(n): \mathbb{Z} \rightarrow \mathbb{R}$ defined only at integer points, often written as $f_n$.
+
+The [Nyquist–Shannon sampling theorem](https://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem) states that a signal with no frequency components higher than half the sample rate $f_{sr}$ can be sampled and reconstructed without losing information.
+In other words, if you bandlimit a signal (with a brickwall lowpass filter at $f_{sr}/2$) and sample points at $f_{sr}$, you can reconstruct the bandlimited signal by finding the unique signal which passes through all points and has no frequency components higher than $f_{sr}/2$.
+
+In practice, digital-to-analog converters (DACs) apply an approximation of a brickwall lowpass filter to remove frequencies higher than $f_{sr}/2$ from the signal.
+The signal is integrated for a small fraction of the sample time $1/f_{sr}$ to obtain an approximation of the amplitude at a point in time, and this measurement is quantized to the nearest digital value.
+
+Analog-to-digital converters (ADCs) convert a digital value to an amplitude and hold it for a fraction of the sample time.
+A [reconstruction filter](https://en.wikipedia.org/wiki/Reconstruction_filter) is applied, producing a signal close to the original bandlimited signal.
+High-quality ADCs may include digital upsampling before reconstruction .
+[Dithering](https://en.wikipedia.org/wiki/Dither) may be done but is mostly unnecessary for bit depths higher than 16.
+
+Of course, noise may also be introduced in each of these steps.
+Fortunately, modern DACs and ADCs as cheap as $2-5 per chip can digitize and reconstruct a signal with a variation beyond human recognizability, with signal-to-noise (SNR) ratios and total harmonic distortion (THD) lower than -90dBr.
+
+
+### Aliasing
+
+The Nyquist–Shannon sampling theorem requires the original signal to be bandlimited at $f_{sr}/2$ before digitizing.
+If it is not, reconstructing will result in an entirely different signal, which usually sounds ugly and is associated with poor-quality DSP.
+
+Consider the high-frequency sine wave in red.
+If the signal is sampled every integer, its unique reconstruction is the signal in blue, which has completely different harmonic content as the original signal.
+If correctly bandlimited, the original signal would be zero (silence), and thus the reconstruction would be zero.
+
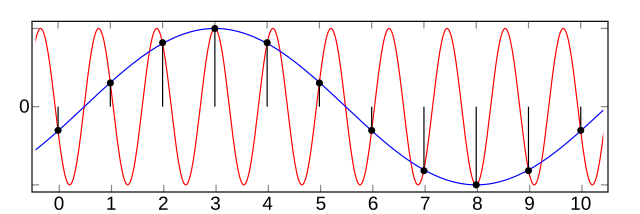+[![](https://upload.wikimedia.org/wikipedia/commons/thumb/2/28/AliasingSines.svg/640px-AliasingSines.svg.png)](https://en.wikipedia.org/wiki/File:AliasingSines.svg)
+
+A square wave has harmonic amplitudes $\frac{1}{k}$ for odd harmonics $k$.
+However, after bandlimiting, all harmonics above $f_{sr}/2$ become zero, so its reconstruction should look like this.
+
+[![](https://upload.wikimedia.org/wikipedia/commons/thumb/b/b3/Gibbs_phenomenon_50.svg/640px-Gibbs_phenomenon_50.svg.png)](https://en.wikipedia.org/wiki/File:AliasingSines.svg)
+
+The curve produced by a bandlimited discontinuity is known as the [Gibbs phenomenon](https://en.wikipedia.org/wiki/Gibbs_phenomenon).
+A DSP algorithm attempting to model a jump found in sawtooth or square waves must include this effect, such as by inserting a minBLEP or polyBLEP signal for each discontinuity.
+Otherwise higher harmonics, like the high-frequency sine wave above, will pollute the spectrum below $f_{sr}/2$.
+
+Even signals containing no discontinuities, such as a triangle wave with harmonic amplitudes $(-1)^k / k^2$, must be correctly bandlimited or aliasing will occur.
+One possible method is to realize that a triangle wave is an integrated square wave, and an integrator is just a filter with a -20dB per [decade](https://en.wikipedia.org/wiki/Decade_(log_scale)) slope.
+Since linear filters commute, a bandlimited integrated square wave is just an integrated bandlimited square wave.
+
+The most general approach is to generate samples at a high sample rate, apply a FIR or polyphase filter, and downsample by an integer factor (known as decimation).
+
+For more specific applications, more advances techniques exist for certain cases.
+Aliasing is required for many processes, including waveform generation, waveshaping, distortion, saturation, and typically all nonlinear processes.
+It is sometimes *not* required for reverb, linear filters, audio-rate FM of sine signals (which is why primitive digital chips in the 80's were able to sound reasonably good), mixing signals, and most other linear processes.
+
+
+### Linear filters
+
+A linear filter is a operation that applies gain depending on a signal's frequency content, defined by
+$$Y(s) = H(s) X(s)$$
+where $s = i \omega$ is the complex angular frequency, $X$ and $Y$ are the [Laplace transforms](https://en.wikipedia.org/wiki/Laplace_transform) of the input signal $x(t)$ and output signal $y(t)$, and $H(s)$ is the [transfer function](https://en.wikipedia.org/wiki/Transfer_function) of the filter, defining its character.
+Note that the [Fourier transform](https://en.wikipedia.org/wiki/Fourier_transform) is not used because of time causality, i.e. we do not know the future of a signal.
+The filter is "linear" because the filtered sum of two signals is equal to the sum of the two individually filtered signals.
+
+A log-log plot of $H(i \omega)$ is called a [Bode plot](https://en.wikipedia.org/wiki/Bode_plot).
+
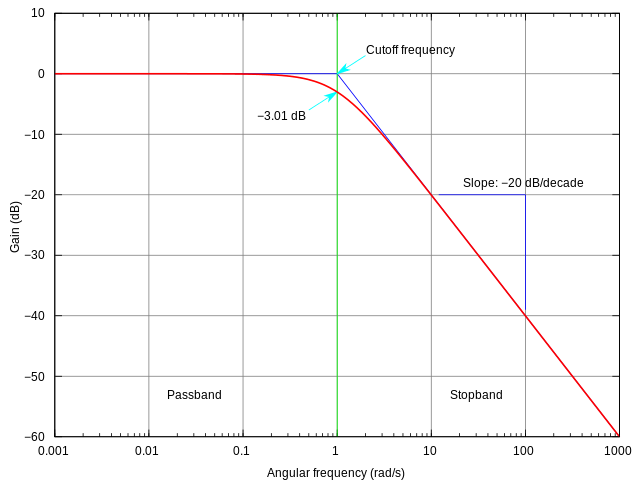+[![](https://upload.wikimedia.org/wikipedia/commons/thumb/6/60/Butterworth_response.svg/640px-Butterworth_response.svg.png)](https://en.wikipedia.org/wiki/File:Butterworth_response.svg)
+
+To be able to exploit various mathematical tools, the transfer function is often written as a rational function in terms of $s^{-1}$
+$$H(s) = \frac{\sum_{p=0}^P b_p s^{-p}}{\sum_{q=0}^Q a_q s^{-q}}$$
+where $a_q$ and $b_p$ are called the *analog filter coefficients*.
+With sufficient orders $P$ and $Q$ of the numerator and denominator polynomial, you can approximate most linear analog filters found in synthesis.
+
+To digitally implement a transfer function, define $z$ as the operator that transforms a sample $x_n$ to its following sample, i.e. $x_{n+1} = z[x_n]$.
+We can actually write this as a variable in terms of $s$ and the sample time $T = 1/f_{sr}$.
+(Consider a sine wave with angular frequency $\omega$. The $z$ operator shifts its phase as if we delayed by $T$ time.)
+$$z = e^{sT}$$
+
+A first order approximation of this is
+$$z = \frac{e^{sT/2}}{e^{-sT/2}} \approx \frac{1 + sT/2}{1 - sT/2}$$
+and its inverse is
+$$s = \frac{1}{T} \ln{z} \approx \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}}$$
+
+This is known as the [Bilinear transform](https://en.wikipedia.org/wiki/Bilinear_transform).
+In digital form, the rational transfer function is written as
+$$H(z) = \frac{\sum_{n=0}^N b_n s^{-n}}{\sum_{m=0}^M a_m s^{-m}}$$
+Note that the orders $N$ and $M$ are not necessarily equal to the orders $P$ and $Q$ of the analog form, and we obtain a new set of numbers $a_m$ and $b_n$ called the *digital filter coefficients*.
+
+The *zeros* of the filter are the nonzero values of $z$ which give a zero numerator, and the *poles* are the nonzero values of $z$ which give a zero denominator.
+A linear filter is stable (its [impulse response](https://en.wikipedia.org/wiki/Impulse_response) converges to 0) if and only if all poles lie strictly within the complex unit circle, i.e. $|z| < 1$.
+
+We should now have all the tools we need to digitally implement any linear analog filter response $H(s)$ and vise-versa.
+
+#### FIR filters
+
+A finite impulse response (FIR) filter is a digital filter with $M = 0$ (a transfer function denominator of 1). For an input $x_k$ and output $y_k$,
+$$y_k = \sum_{n=0}^N b_n x_{k-n}$$
+They are computationally straightforward and always stable since they have no poles.
+
+Long FIR filters ($N \geq 128$) like FIR reverbs (yes, they are just linear filters) can be optimized through FFTs.
+Note that the above formula is the convolution between vectors $y$ and $b$, and by the [convolution theorem](https://en.wikipedia.org/wiki/Convolution_theorem),
+$$y \ast b = \mathcal{F}^{-1} \{ \mathcal{F}\{y\} \cdot \mathcal{F}\{b\} \}$$
+where $\cdot$ is element-wise multiplication.
+
+While the naive FIR formula above is $O(n^2)$ when processing blocks of $n$ samples, the FFT FIR method is $O(\log n)$.
+A disadvantage of the FFT FIR method is that the signal must be delayed by $N$ samples to produce any output.
+You can combine the naive and FFT methods into a hybrid approach with the [overlap-add](https://en.wikipedia.org/wiki/Overlap%E2%80%93add_method) or [overlap-save](https://en.wikipedia.org/wiki/Overlap%E2%80%93save_method) methods.
+
+#### IIR filters
+
+An infinite impulse response (IIR) filter is a general rational transfer function. Applying the $H(z)$ operator to an input and output signal,
+$$\sum_{m=0}^M a_m y_{k-m} = \sum_{n=0}^N b_n x_{k-n}$$
+Usually $a_0$ is normalized to 1, and $y_k$ can be written explicitly.
+$$y_k = \sum_{n=0}^N b_n x_{k-n} - \sum_{m=1} a_m y_{k-m}$$
+
+For $N, M = 2$, this is a [biquad filter](https://en.wikipedia.org/wiki/Digital_biquad_filter), a very fast, numerically stable, and reasonably good sounding filter.
+
+$$H(z) = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}}$$

README.md

@@ -8,6 +8,8 @@ Send a pull request to this repository with your edits.
 Major changes like new pages and complete overhauls are welcome, as well as minor fixes like grammar, spelling, and reorganization.
 Your PR will be accepted if it is a net positive benefit to readers.
 
+The LaTeX renderer supports [these functions](https://khan.github.io/KaTeX/function-support.html).
+
 ### Building
 
 Install [Node](https://nodejs.org/en/). Make sure `npm` is in your PATH.

Toolbar.md

@@ -5,9 +5,9 @@
 When power meters are enabled, Rack measures the amount of time spent processing each module in *mS* (millisamples).
 In many ways, this is analogous to the module power limit imposed by hardware modular synthesizers in *mA* (milliamperes).
 
-The total amount of time spent processing all modules must equal **1000 mS**.
+To maintain a stable audio clock, the total amount of time spent processing all modules must equal **1000 mS**.
 To achieve this, the [Audio](Core.md#audio) module from [Core](Core.md) uses your audio device's high-precision clock to regulate Rack's processing loop, so it idles for some amount of mS until this total is met.
-If the Audio idle time falls to an average of 0 mS over its block size, an audio stutter will occur.
+If the Audio idle time falls close to an average of 0 mS over its block size, an audio stutter may occur.
 This can be caused by other modules consuming lots of mS.
 
 ### Internal sample rate